SC&RA Official Magazine

International Cranes & Specialized Transport and American Cranes & Transport are the official magazines of the Specialized Carriers & Rigging Association.
The partnership gives readers and advertisers a strategic advantage, plus access to exclusive information and industry events.
the Specialized Carriers & Rigging Association.
The partnership gives readers and advertisers a strategic advantage, plus access to exclusive information and industry events.
Visit the SC&RA home page

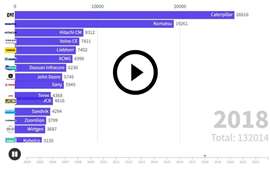
Exclusive, searchable online directory of cranes, covering 110 manufacturers and 9,300 individual products, including detailed specifications.
Visit now
The gold standard in market research
Off-Highway Research offers a library of more than 200 regularly updated reports, providing forensic detail on key aspects of the construction equipment industry.
Our detailed insights and expert analyses are used by over 500 of the world’s largest and most successful suppliers, manufacturers and distributers, to inform their strategic plans and deliver profitable growth.
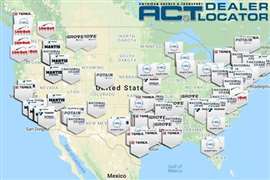
Visit the Dealer Locator and search by manufacturer to find the right piece of equipment in your local area.
Locate your nearest crane dealer
The Legendary Book

The Legendary! book is out. Commemorating the 75th anniversary of
the SC&RA, the beautifully illustrated book
features the history of the SC&RA and the legendary jobs, equipment, people and events that made the
rigging, lifting and specialized transportation sector what it is today.
Order your copy here
AC&T Sourcebook 2024

The 2024 ACT Sourcebook is the most respected reference guide for the crane, rigging and specialized transportation sector – containing specs for all of the cranes and transport equipment distributed in North America.
Download now