How are sling forces affected by inclining a beam during a lift?
27 February 2023
When installing an inclined beam how do the sling forces change? Specialist technical contributor Keith Anderson considers the question.
 Wiesbauer’s Liebherr LG 1750 mobile lattice boom crane dismantling pedestrian bridge as part of the Stuttgart 21 rail project in Germany
Wiesbauer’s Liebherr LG 1750 mobile lattice boom crane dismantling pedestrian bridge as part of the Stuttgart 21 rail project in Germany
I was recently asked a question relating to the installation of a long beam. The beam was to be lifted with one crane using a pair of slings and it had to be installed with one end lower than the other.
The intention was to lift it horizontally then touch down one end on its support before letting it rotate about that point as it was lowered further until the other end came to bear on its support.
 What happens when you switch from horizontal, left, to an inclined beam?
What happens when you switch from horizontal, left, to an inclined beam?
The question was “what happens to the sling loads” when you do this. It is a reasonable question because you want to size the slings, lugs and hardware adequately.
I couldn’t immediately answer it so I had a think about it for a while.
Initial lifts
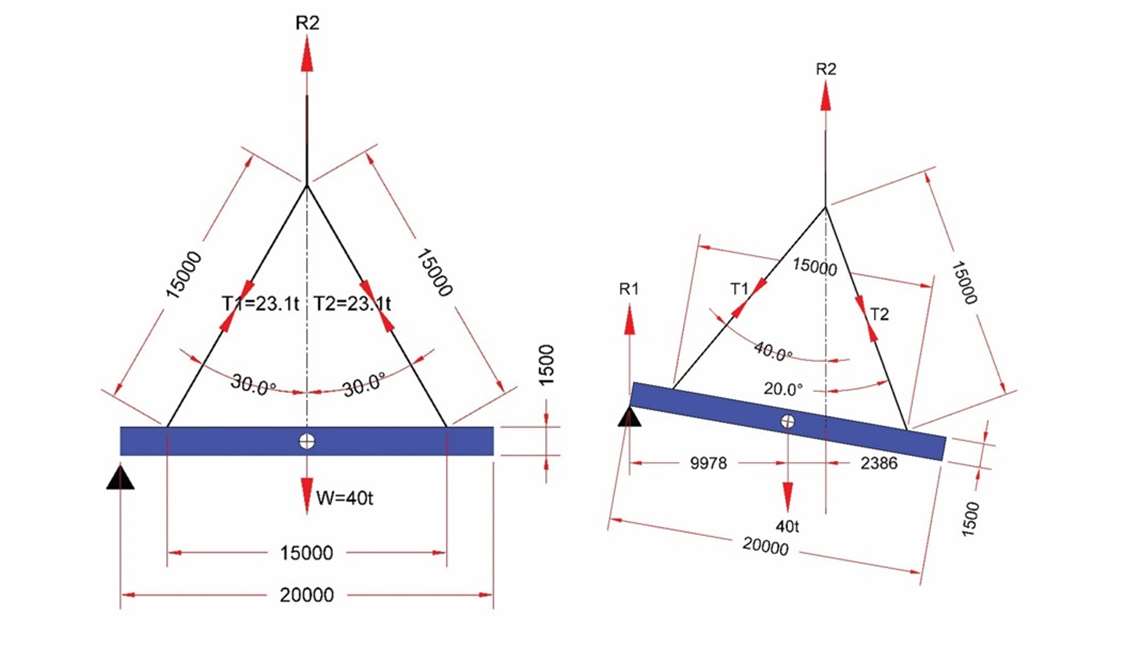
First, as a base point, what are the sling tensions when the beam is initially lifted horizontally?
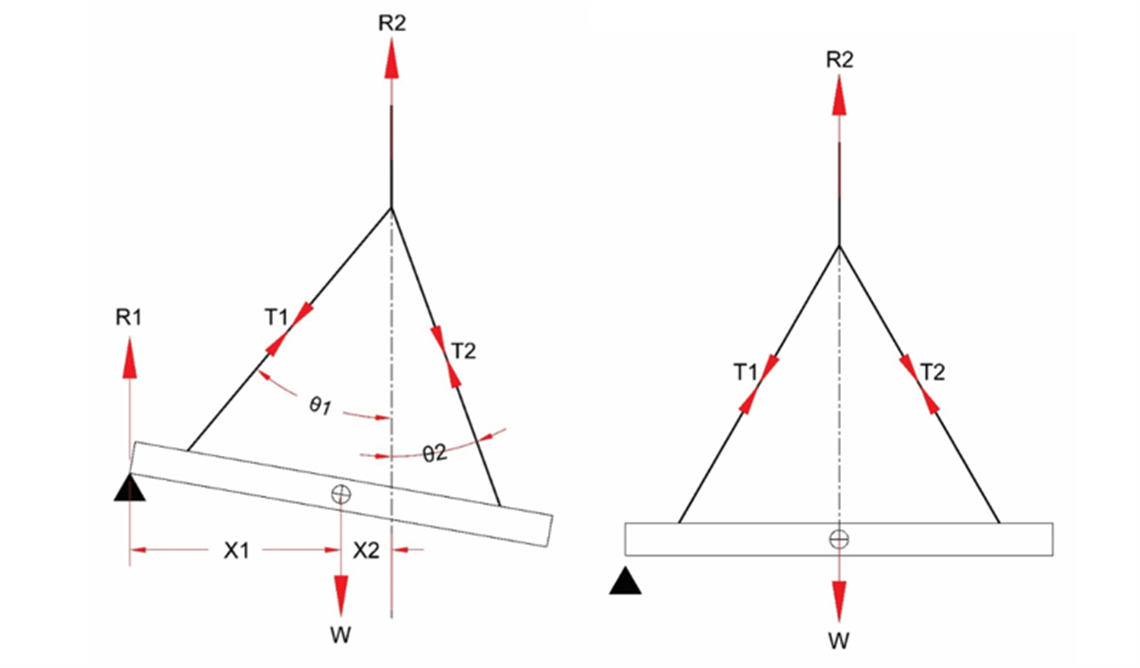
For this exercise, I have taken the centre of gravity (C of G) of the beam to be at the geometric centre of the beam and the two equal length suspension slings to be at 30° to the vertical, attached to lugs on the upper surface of the beam equidistantly about the C of G. The (high) support is shown to the left.
Initially, the vertical load to the crane R2 = W; the vertical load to each lug is 0.5W. The sling tensions are equal and are given by the following equation: T1 = T2 = 0.5W/cos θ
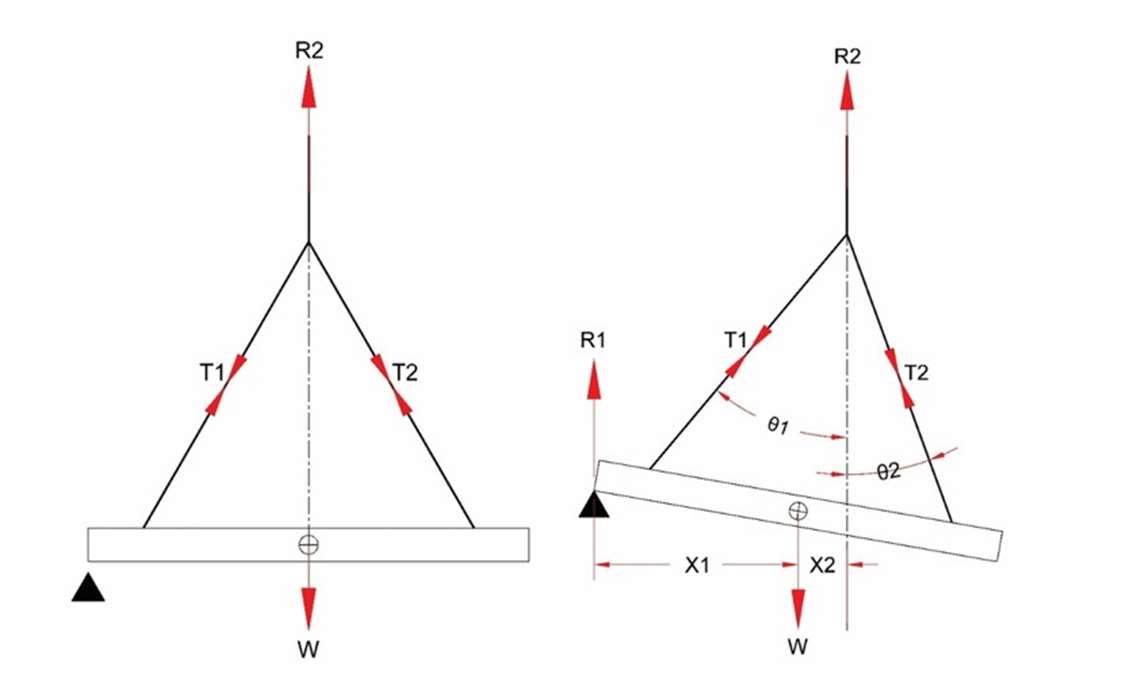
- How does this change as the beam is touched down on the support? (It is assumed that this point acts as a rocker only, with no horizontal load carrying ability). The hoist lines are kept vertical.
- As the beam is progressively lowered, the support starts to accept load and the beam rotates about that point. The point at which the slings meet (the crane hook) moves to the right and the line of action of R2 is no longer above the C of G.
- The load to the crane reduces slightly and the vertical reaction at the support increases by the same amount.
The crane load (vertical force) is shared unequally between the two lift lugs with Lug 2 seeing more and Lug 1 less. As Sling 2 becomes more vertical, its tension is more effective in providing vertical support to the beam.
In summary, as the beam tilts there are opposing effects, two that work to decrease the tension in Sling 2 and one that tends to increase it. Which effects are more dominant and how does it change as the tilt increases?
We can see how these opposing effects play out by modelling the forces mathematically. Results will, of course, be determined by input variables such as the weight, the length and depth of the beam, the sling lengths and the location of the lifting lugs.
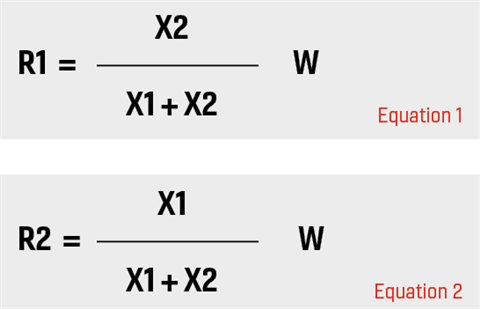
Playing about with the inputs should give a feel as to how it all works and yield trends that can inform us. So, how is the weight shared (vertically) between the crane and the support?
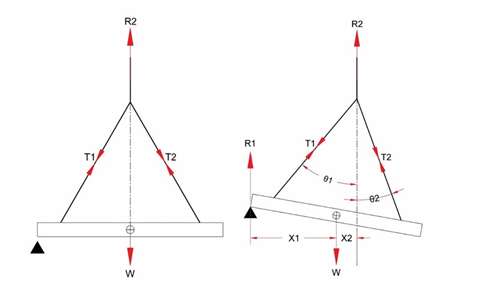
The reactions are in the inverse proportion of their horizontal distances from the C of G.
Analysis is easiest by looking at the force balance at the crane hook; the crane load is opposed by the sum of the vertical components of the sling tensions.

For equilibrium, the horizontal components of the sling tensions must be equal and opposite.
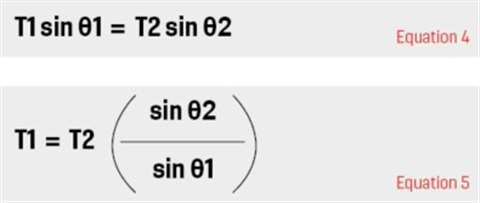
Substituting for T1 from Eq.5 in Eq.3 gives:
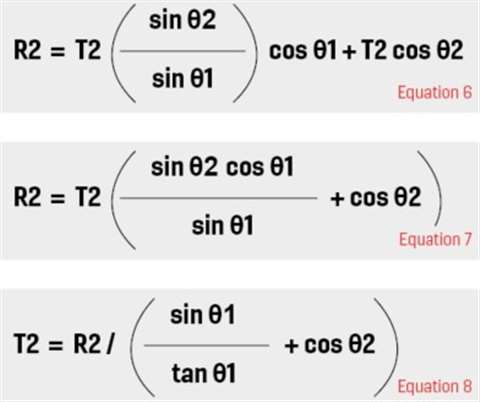
Drawing the arrangement at the angle of interest, X1, X2, θ1 and θ2 can be measured and, as the weight is known, all the variables are available to allow T2 to be calculated.
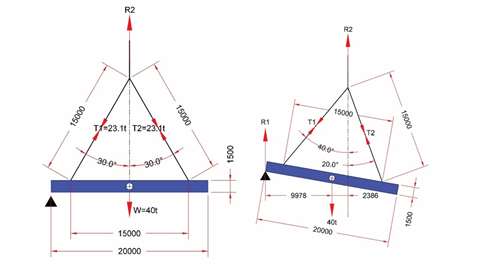 Example A
Example A
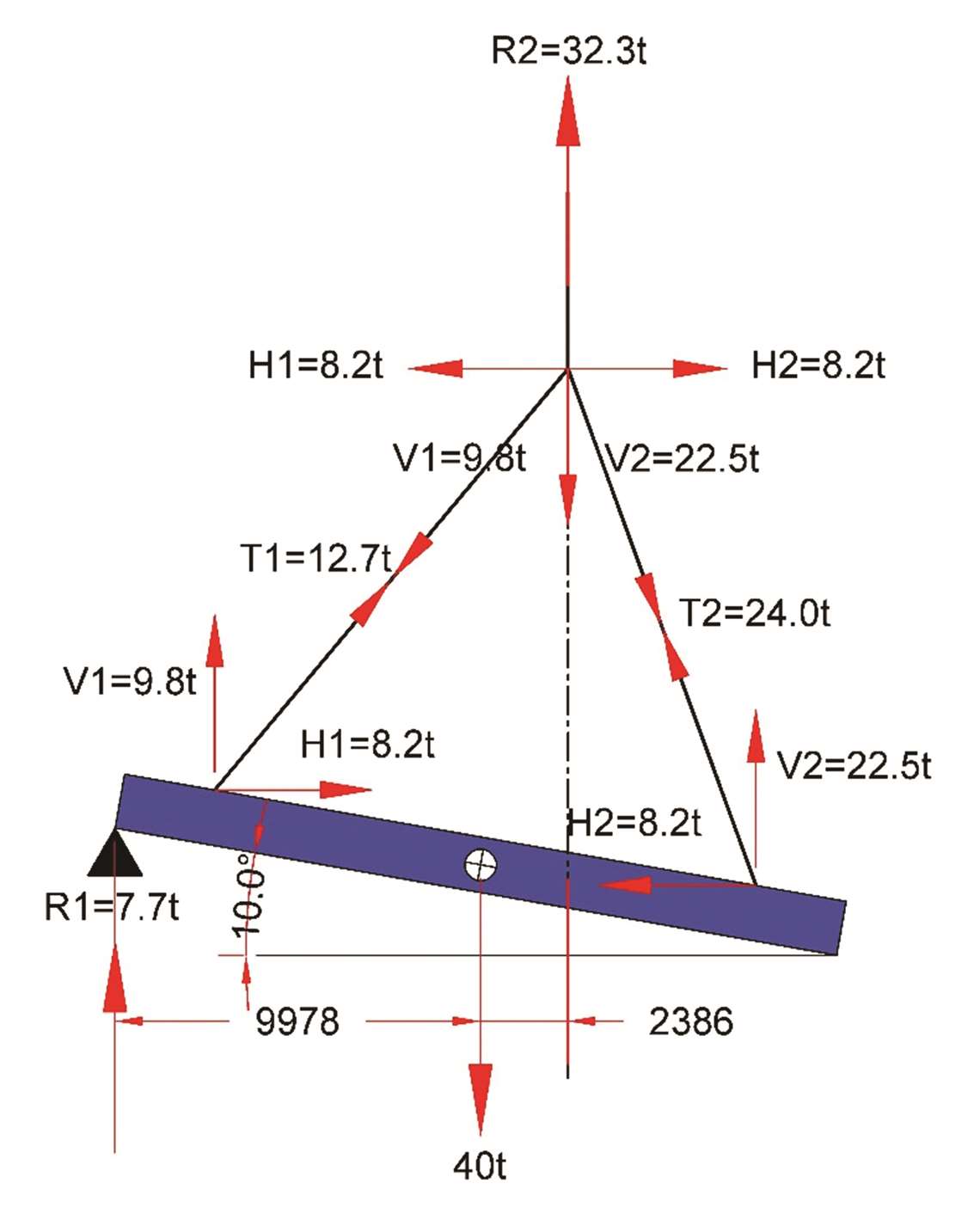
Example A: Assume a beam 20 metres long x 1.5 metres deep weighing 40 tonnes; C of G central with lugs equidistant about the C of G at 15 metre centres.
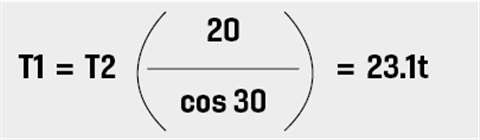
15 metre-long slings are to be used. When horizontal:
When inclined at a maximum of 10°, X1 = 9,978 mm, X2 = 2,386 mm, θ1 = 40° & θ2 = 20°. Inputting in Equations 1,2 & 8 yields:

And therefore:

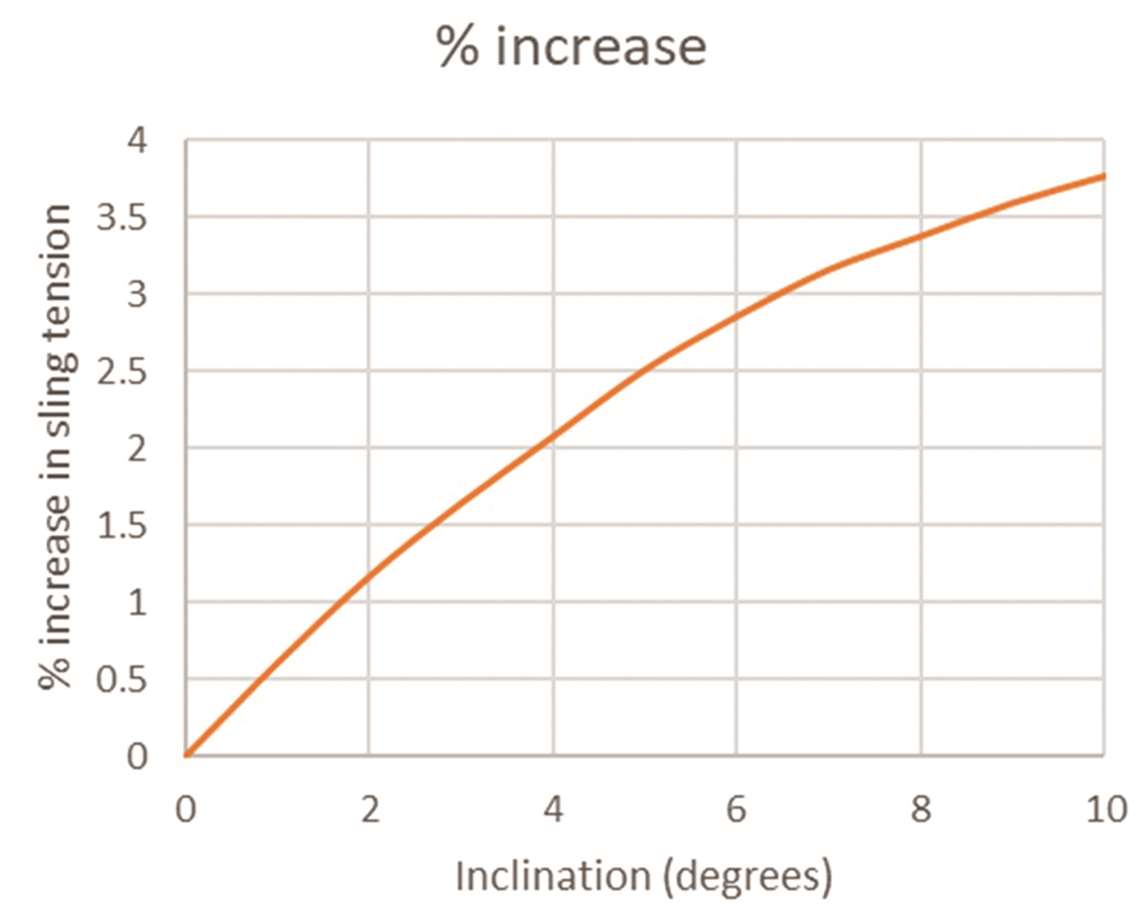
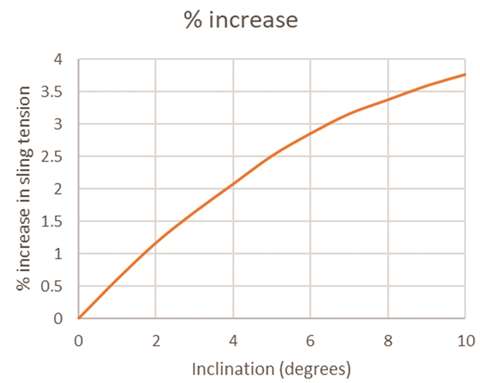 % increase in sling tension
% increase in sling tension
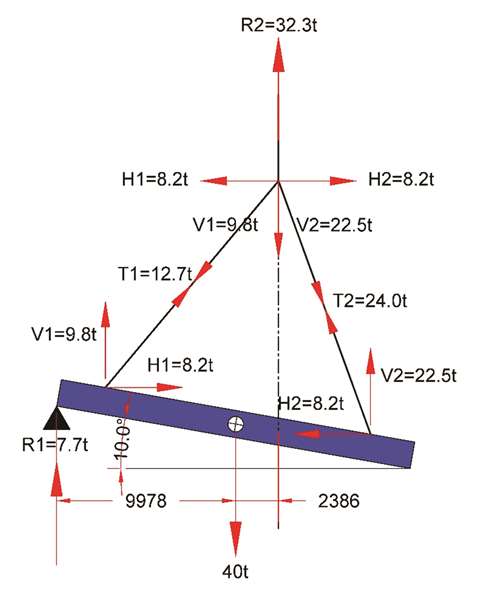
T2 when horizontal was 0.5775 x 40 = 23.1t, so 24.0t, (diagram, right), represents a 3.75 % increase in tension in that sling over when the beam was horizontal.
The reduction in the load to the crane and the increased efficiency of Sling 2 is not quite enough to offset the increase in percentage of the crane load carried by Lug2.
Plotting the percentage increase in tension, left, for our example from 0 to 10° shows that the rate of increase in tension decreases as the inclination increases.
Effect of varying the geometry
So, we have seen with the geometry in the example, that there is a modest increase in tension in the “downhill” sling when the beam is tilted.
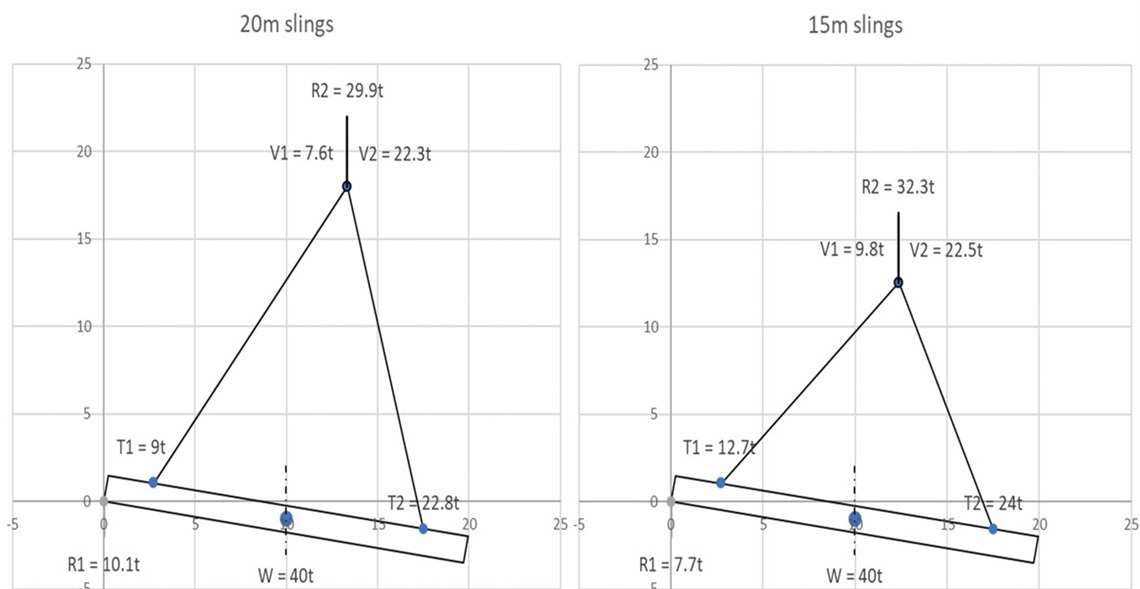
What happens if we use longer slings? (Using a spreadsheet makes it easy to change the inputs).
When longer slings are used, the point at which they meet – the hook block location – is higher relative to the beam. When the beam is tilted the line of action of the crane moves proportionally further to the right, resulting in more load on the support and less on the crane.
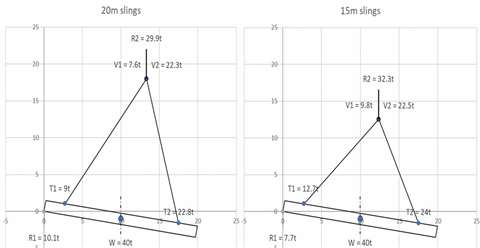 Longer slings means where they meet is higher
Longer slings means where they meet is higher
The RH sling is also more vertical. The net effect is that the RH sling tension is reduced and is in fact now slightly less than it was when the beam was horizontal.
Take aways
In conclusion, the tension in the downhill sling is a function of the geometry of the beam and the way it is rigged.
Given typical proportions and sling lengths, when the beam is tilted, the tension may modestly increase from that when horizontal.
If longer slings are used; when tilted, the tension may be less. The shorter the slings, the greater the increase in tension.
If conducting this type of operation, it is recommended that you use the equations provided to calculate the tensions when inclined and size the slings, hardware and lugs accordingly.
STAY CONNECTED


Receive the information you need when you need it through our world-leading magazines, newsletters and daily briefings.